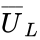Tracer flow in porous reservoir rock

Selecting the appropriate tracer, and understanding the information gathered during a well to well tracer test requires consideration of how various tracers interact with, and therefore flow, through reservoir rock. This article discusses these considerations and the necessary mathematical calculations.

Retention caused by partitioning between phases

When tracers are flowing in the reservoirs, it is normally a requirement that the compounds follow the phase they are going to trace. The best example of a passive water tracer is tritiated water (HTO). The HTO will, in all practical aspects, follow the water phase.

For gas tracers, there are no known passive tracers. All gas compounds will, to a certain degree, partition between the phases. The most ideal gas tracer is tritiated methane. This gas tracer follows the methane component in the gas phase closely, and the pressure-volume-temperature (PVT) properties of this gas tracer can be found with ordinary PVT calculations. The properties of the other radioactive hydrocarbon gas tracers may be found with the same PVT calculations by examining their respective nonradioactive homologues.

In Fig. 1, the flowing properties of a selection of some gas tracers are compared. These tracers were tested in a 12-m-long slimtube with an inner diameter of 0.5 cm. The filling material was crushed Ottawa sand. Tritiated methane, CH₃T, was the reference tracer. The oil saturation in the experiments is 30% and the production curve, when a small slug of tracer is flowing through a porous medium, is measured. All tracers, even the tritiated methane, are delayed with respect to the average flow rate in the reservoir. A nonpartitioning tracer would have been produced after one pore volume (PV) (available gas volume) had been flushed through the system.

• 

  Fig. 1 – Tracer-retention experiments in a pack column of Ottawa sand. Gas tracers are compared at two different conditions (after Dugstad).

Normally, the K_C values (see Eq. 1) decrease and, thereby, the variations in retention time are reduced when the pressure is increased. The K_P value (see Eq. 2) converges to 1 for all compounds when miscible conditions are obtained. The separation of the tracer production curves is reduced considerably in Fig. 1b when the pressure increases from 150 to 250 bar. It also is observed that the ethane tracer, ¹⁴CH₃CH₃, is produced before that of the perfluoromethylcyclopentane (PMCP) at 150 bar while, at 250 bar, PMCP is in front of ethane. The partitioning properties of the perfluorocarbon (PFC) have different characteristics than the partitioning properties of the hydrocarbons.

Water tracers, like gas tracers, may partition to the oil phase. Many water tracers exist that behave almost as ideal tracers. Fig. 2 shows laboratory tests in which some benzoic acid tracers are compared with the HTO. These experiments are carried out in a packed column of 2-m length. The packing material was crushed Berea sandstone. Other types of equipment also are used frequently. It is common to use cores of consolidated reservoir or reservoir-like rock, for example:

• Sandstones
• Carbonate material

• 

  Fig. 2 – Tracer-dispersion curves of (a) 2-fluorobenzoic acid and (b) 3-trifluoromethyl-benzoic acid compared with tritiated water from flooding experiments in sandstone (after Bjørnstad et al.

Retention factors, β, may be derived from Eq. 1 on the basis of the production profiles found by such experiments.

$1+\beta ={\frac {V_{T}}{V_{S}}},$

(1)

where V_T is the retention volume for the tracer candidate and V_S is the retention volume for the standard reference tracer. The retention volume for the standard reference tracer (nonpartitioning) may further be regarded as the volume of the mobile phase, V_M, in this system. If other retention effects can be excluded, the retention factor is an expression for the delay caused by partitioning the tracer between the mobile and the stationary phase.

Partition coefficients

The partition coefficient depends on the temperature and pressure as well as the composition of the system. Unlike the radioactively labeled hydrocarbons, the partition coefficient of the PFC gas tracers are not easily obtained. The equation of state (EOS) used in PVT calculations is not optimized for these types of compounds, and lack of interaction parameters makes partition coefficient estimation on the basis of the EOS difficult. Normally, laboratory measurements are necessary.

When the composition, temperature, and pressure are given, each component will have a given partitioning coefficient at equilibrium. This component may be defined in different ways. Two different definitions are used frequently for gas/oil systems:

$K_{C}\equiv {\frac {C_{O}}{C_{G}}}$

(2)

and

$K_{P}\equiv {\frac {y_{i}}{x_{i}}}$

(3)

C_O = the tracer concentration in the oil phase, and C_G = the tracer concentration in the gas phase. The partition coefficient, K_P, is calculated by dividing the mole fraction of the tracer in the gas phase, y_i, by the mole fraction of the tracer in the oil phase, x_i.

When the molar composition and the densities of the two phases are known, the relation between the two values can be expressed as

$K_{C}={\frac {\delta _{O}\sum y_{i}M_{W}}{\delta _{G}\sum x_{i}M_{W}}}\cdot {\frac {1}{K_{P}}}$

(4)

For simple systems, partition coefficients can be found when the vapor pressure, p_v, of the tracer compound is known. At low pressure, the partitioning between the phases will obey Henry’s law, and the Henry’s law constant, H_C, is

$H_{C}={\frac {p_{i}}{x_{i}}}$

(5)

In the case in which Raoult’s law is valid (ideal behavior), the partial pressure, p_i, of the component in the gas phase is given as

$p_{i}=x_{i}p_{\nu }$

(6)

and

$y_{i}={\frac {p_{i}}{p}},$

(7)

where p is the total pressure. Combining these two equations gives

${\frac {y_{i}}{x_{i}}}={\frac {p_{\nu }}{p}}=K_{p}$

(8)

The vapor pressure of the pure component divided by the total pressure gives the K_P value. This relation will normally be too simple to be accurate but may have sufficient validity to carry out a rough estimate.

Flow equations when one phase is mobile

The partition coefficient may be measured directly by measuring the concentration of the component in each of the two phases in an equilibrium system.

In a dynamic situation, the K_C value can be found by measuring the retention time of the actual component. K_C values can be calculated when the saturation and the retention time are known. In a dynamic column experiment in which the column contains only two phases (one stationary), the fraction of time, t_f, the tracer stays in the gas phase may be expressed as the number of tracer molecules in the gas phase in a reference block of the column divided by the total number of tracer molecules in the same reference block.

$t_{f}={\frac {C_{M}V_{M}}{C_{M}V_{M}+C_{S}V_{S}}}$

(9)

Dividing by C_MV_M above and below the fraction time and inserting Eq. 2 leads to

$t_{f}={\frac {1}{1+K_{C}\left({\frac {V_{S}}{V_{M}}}\right)}}$

(10)

C_M and C_S are tracer concentrations in mobile and stationary phases, respectively. The tracer is produced when one retention volume, V_T, has been injected. This volume multiplied by the fraction of the time the tracer stays in the mobile phase is equal to the volume of the mobile phase, V_M, in the system.

$t_{f}={\frac {V_{M}}{V_{T}}}$

(11)

A combination of Eqs. 10 and 11 gives

$K_{C}={\frac {(V_{T}-V_{M})}{V_{S}}}$

(12)

Assuming steady-state flow, V_T/V_S may be replaced by the t_T/t_S, where t_T and t_S are the retention time of the partitioning tracer and the nonpartitioning reference tracer, respectively. Applying Eqs. 13 and 14 and rearranging, the oil saturation in the flooded porous medium can be estimated (with retention factor β found in Eq. 1) by Eq. 15.

$V_{p}=V_{S}+V_{M},$

(13)

$S_{o}={\frac {V_{S}}{V_{p}}},$

(14)

and

$S_{o}={\frac {1}{K_{C}/\beta +1}}$

(15)

In Eq. 13, V_S is assumed to be the volume of the oil phase.

Flow equations when two phases are mobile

Eqs. 9 through 15 assume one mobile and one stationary phase. For a generic two-phase case, the tracer flow equation may be expressed in a dimensionless form where S = saturation, C = concentration, K = partition coefficient, and f = fractional flow and when dispersion is neglected.

${\frac {\partial }{\partial t^{*}}}\{[S+(1-S)K]C\}+{\frac {\partial }{\partial x^{*}}}\{[f+(1-f)K]C\}=0$

(16)

x* = x/L and t* = (q t) / (a L ϕ) to obtain the dimensionless form of the system.

Assuming a two-phase gas/oil system in which the tracers are flowing partly in the gas phase and partly in the oil phase, the linear velocity of the gas and oil phases are given as

${\overline {U}}_{o}=\left({\frac {f_{o}}{S_{o}}}\right)\left({\frac {q}{a\phi }}\right)$

(17)

and

${\overline {U}}_{g}=\left({\frac {f_{g}}{S_{g}}}\right)\left({\frac {q}{a\phi }}\right),$

(18)

where f_o and f_g are the fractional flow of oil and gas, respectively, and q = volumetric flow rate, ϕ = porosity, and a = flow cross section. As previously shown, the fraction of time the tracer stays in the gas may be expressed by Eq. 9. The mean velocity of the tracer in a two-phase flow may be expressed by Eq. 19 when accepting that V_S/V_M is equal to S_o/S_g.

${\overline {U}}_{tr}=\left\{\left({\frac {f_{g}}{S_{g}}}\right){\frac {1}{1+K_{C}\left({\frac {S_{o}}{S_{g}}}\right)}}+\left({\frac {f_{o}}{S_{o}}}\right)\left[1-{\frac {1}{1+K_{C}\left({\frac {S_{o}}{S_{g}}}\right)}}\right]\right\}\left({\frac {q}{a\phi }}\right)$

(19)

Rearrangement gives

${\overline {U}}_{tr}=\left({\frac {f_{g}+K_{C}f_{o}}{S_{g}+K_{C}S_{o}}}\right)\left({\frac {q}{a\phi }}\right)=f_{t}\left({\frac {q}{a\phi }}\right)$

(20)

This tracer-flow-velocity model may be applied when the K_C values are known. Fig. 3 gives a graphical outline of f_t (based on Eq. 20) for five different partitioning coefficients. The fractional flow curve for the gas, f_g, is arbitrarily chosen. The f_t curves = 1 at the saturation where f_o/S_o = f_g/S_g (i.e., when both phases are flowing with the same linear velocity). When the K_c value=1, the tracer flow rate is independent of saturation and shape of the fractional flow curve. The f t curves plotted in Fig. 3 show that the relative flow of the tracers depends strongly on the saturation. Below the gas saturation at which the two phases flow with the same linear velocity, the lower-partitioning tracers will be in front while above that saturation decreasing K_c value will give increasing flow rate.

• 

  Fig. 3 – Relative tracer flow rates in a two-phase system for a certain fractional flow curve (after Dugstad, Bjørnstad, and Hundere).

Residual-oil measurements

Eqs. 9 through 20 give the basis for estimating remaining oil in the reservoir. In the most simple system, in which the oil saturation is stationary, S_o may be calculated from the knowledge of the partition coefficient of two tracers and the peak of the tracer-response curve by

$S_{o}={\left[\left({\frac {V_{Ti}K_{ci}-V_{Tj}K_{cj}}{V_{Tj}-V_{Ti}}}\right)+1\right]}^{-1}$

(21)

Under ideal conditions, V_T may be replaced by the retention time of the two tracers. There is always a question about which retention time to use in the calculations. Alternatives are breakthrough, production peak, moment (mass middle point), or other specific landmarks. The production curve is a superposition of contribution from individual streamtubes in the reservoir; therefore, the choice of retention time will reflect either saturations in certain streamtubes or an average value. A sensitivity evaluation of Eq. 21 shows that it is preferable to apply two tracers with K_C values far apart from each other. The most efficient would be to include one tracer that has no partitioning to the liquid phase. Eq. 21 then is simplified to Eq. 15.

One of the questions that may be raised against the method is the possibility for obtaining equilibrium between the phases. The calculations are based on a real equilibrium between the phases, which depends on saturation, diffusion rates, flow rates, pore structure, and partition coefficient.

To obtain reliable results, it is crucial to understand the flow situation. If the oil phase is stationary, Eq. 21 may give a satisfactorily result. If two phases are flowing, it is important to know the fractional flow curves (i.e., relative permeability), and a reservoir simulator will be necessary to obtain a reliable result.

Biodegradation

Microbial stability of water tracers may be a problem. This problem will be less important at higher temperatures at which the microbial activity is lower. The problem, however, must be addressed in sample handling and storage. Some tracers, in special situations, may biodegrade after sampling. To avoid such degradation, a biocide may be added to the sample immediately after collection. Adding 0.1 ppm NaN₃ to the stock solution can prevent bacterial growth.

Fluorobenzoic acid tracers have been reported to biodegrade when exposed to seawater. The biodegradation has been measured for monofluorobenzoic acid and di- and tri-fluorobenzoic acid. No degradation was observed for the di- and tri-fluor compounds. Alcohols also may biodegrade under certain conditions. In general, the odd-carbon-number alcohols are more resistant to bacterial attack than the even-number ones.

Ion exchange

Ions adsorbed on the reservoir surface are free to exchange with ions in the water. This ion exchange is a reversible process and tends to obtain equilibrium between surface concentration and the concentration in the water. Different adsorption isotherms may be used to describe this situation. In most cases, this ion exchange can be described by a Langmuir isotherm (Eq. 22).

The flow of the tracer through the reservoir may be influenced by adsorption to the grain surface. To come into contact with the grain surface, the gas tracer may need to diffuse through a film of oil, water, or both. The adsorption depends on the partitioning of the tracer into the two liquid phases in the reservoir. Different models are applied to describe the adsorption on the grains. The simplest form is the linear relation in which the adsorbed amount, a_c, is proportional to the concentration in the contacting phase C_c.

$a_{c}=K\cdot C_{c}$

(22)

A tracer in a dynamic system will be retained independently of concentration. In many cases, however, the active adsorption sites on the surface will be saturated and the amount adsorbed will not increase linearly with the concentration. In some cases, a more accurate expression is the Langmuir isotherm,

$a_{c}={\frac {U\cdot c}{1+V\cdot c}}$

(23)

U and V are two parameters that decide the shape of the curve for the actual system at a specific temperature. c = the concentration in the liquid phase caused by partitioning between the gas and liquid phase, and a_c = the amount of tracer adsorbed to the grain. At low concentration, which is the case when tracers are considered, this equation will be a straight line with slope U. Other isotherms also may be considered but are less likely to be needed. Different adsorption isotherms will influence the produced tracer peak.

If the tracer is positively charged, it can be exchanged with cations adsorbed to the reservoir surface. The affinity to the surface may vary, and some cations will be more tightly adsorbed than others. The effect on the tracer flow will be retention of the tracer. According to the most likely adsorption isotherm, the adsorption will be linear with the tracer concentration as long as the concentration is very low.

²²Na has shown to move through porous media with only minor delay caused by sorption and ion exchange to reservoir rock but in a reversible manner. Most other cations (Cs⁺, Co³⁺) have shown strong adsorption and cannot be used as tracers.

Nomenclature

a	=	cross section, L2
ac	=	adsorbed amount
A	=	constant related to the enthalpy
c	=	concentration in the liquid phase caused by partitioning between the gas and liquid phase
C	=	concentration
Cc	=	concentration in the contacting phase
CG	=	concentration of tracer in gas phase
CM	=	concentration of tracer in mobile phase
CO	=	concentration of tracer in oil phase
CS	=	concentration of tracer in stationary phase
f	=	fractional flow
fg	=	fractional flow for gas
fo	=	fractional flow for oil
ft	=	flow of tracer (see Eq. 20)
HC	=	Henry’s law constant
k	=	permeability, L2
K	=	partition coefficient
KC	=	partition coefficient based on concentration
Kci	=	partition coefficient of component i
Kcj	=	partition coefficient of component j
KP	=	partition coefficient based on mol fraction
M	=	amount of tracer originally injected
MW	=	molecular weight, m
p	=	pressure, m/Lt2
pi	=	partial pressure, m/Lt2
pv	=	vapor pressure, m/Lt2
q	=	volume flux, L3/t
S	=	saturation
Sg	=	gas saturation
So	=	oil saturation
t	=	time, t
t*	=	dimensionless time
tf	=	fraction of time, t
U	=	parameter that decides the shape of the curve for the actual system at a specific temperature
${\overline {U}}_{g}$	=	average linear flow rate of gas phase, L/t
${\overline {U}}_{L}$	=	average linear flow rate of liquid phase, L/t
${\overline {U}}_{tr}$	=	average velocity of tracer, L/t
V	=	parameter that decides the shape of the curve for the actual system at a specific temperature
VM	=	volume of mobile phase, L3
Vp	=	pore volume, L3
VS	=	retention volume of standard reference tracer, L3
VT	=	retention volume of tracer candidate, L3
VTi	=	retention volume of tracer candidate i, L3
VTj	=	retention volume of tracer candidate j, L3
x*	=	dimensionless distance
xi	=	mole fraction of tracer i in liquid phase
yi	=	mole fraction of tracer i in gas phase
α	=	dispersivity
β	=	retention factor
δG	=	density of gas, m/L3
δO	=	density of oil, m/L3
σ	=	standard deviation
ϕ	=	porosity

Noteworthy papers in OnePetro

Use this section to list papers in OnePetro that a reader who wants to learn more should definitely read

External links

https://www.corelab.com/protechnics/

See also

Well to well tracer tests

Planning and design of well to well tracer tests

Interpreting data from well to well tracer tests

PEH:Well-To-Well_Tracer_Tests