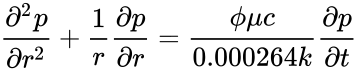Sandbox:Fluid flow in porous media

Introduction

In this initial chapter on fluid flow in porous media, we begin with a discussion of the differential equations that are used most often to model unsteady-state flow. Simple statements of these equations are provided in the text; the more tedious mathematical details are given in Development of differential equations for flow in porous media for the instructor or student who wishes to develop greater understanding. The equations are followed by a discussion of some of the most useful solutions to these equations, with emphasis on the exponential-integral solution describing radial, unsteady-state flow. An appended discussion (Dimensionless variables) of dimensionless variables may be useful to some readers at this point.

The chapter concludes with a discussion of the radius-of-investigation concept and of the principle of superposition. Superposition, illustrated in multiwell infinite reservoirs, is used to simulate simple reservoir boundaries and to simulate variable rate production histories. An approximate alternative to superposition, Horner's "pseudoproduction time," completes this discussion.

The ideal reservoir model

To develop analysis and design techniques for well testing, we first must make several simplifying assumptions about the well and reservoir that we are modeling. We naturally make no more simplifying assumptions than are absolutely necessary to obtain simple, useful solutions to equations describing our situation – but we obviously can make no fewer assumptions. These assumptions are introduced as needed, to combine (1) the law of conservation of mass, (2) Darcy's law, and (3) equations of state to achieve our objectives. This work is only outlined in this chapter; detail is provided in Development of differential equations for flow in porous media and the References.

Consider radial flow toward a well in a circular reservoir. If we combine the law of conservation of mass and Darcy's law for the isothermal flow of fluids of small and constant compressibility (a highly satisfactory model for single-phase flow of reservoir oil), we obtain a partial differential equation that simplifies to

${\partial ^{2}p \over \partial r^{2}}+{1 \over r}{\partial p \over \partial r}={\phi \mu c \over 0.000264k}{\partial p \over \partial t}$

${\partial ^{2}p \over \partial r^{2}}+{1 \over r}{\partial p \over \partial r}={\phi \mu c \over 0.000264k}{\partial p \over \partial t}$

(1.1)

.................... (1.1)

if we assume that compressibility, c, is small and independent of pressure; permeability, k,is constant and isotropic; viscosity, μ, is independent of pressure; porosity, ϕ, is constant; and that certain terms in the basic differential equation (involving pressure gradients squared) are negligible. This equation is called the diffusivity equation;the term 0.000264k/ϕμc is called the hydraulic diffusivity and frequently is given the symbol η.

Eq. 1.1 is written in terms of field units. Pressure, p, is in pounds per square inch (psi); distance, r, is in feet; porosity, ϕ, is a fraction; viscosity, μ, is in centipoise; compressibility, c, is in volume per volume per psi [c = (l/ρ) (dρ/dp)]; permeability, k,is in millidarcies; time, t, is in hours; and hydraulic diffusivity, η, has units of square feet per hour.

A similar equation can be developed for the radial flow of a nonideal gas:

.................... (1.2)

where z is the gas-law deviation factor.

For simultaneous flow of oil, gas, and water,

.................... (1.3)

where c_t is the total system compressibility,

.................... (1.4)

and the total mobility λ_t is the sum of the mobilities of the individual phases:

.................... (1.5)

In Eq. 1.4, S_o refers to oil-phase saturation, c_o to oil-phase compressibility, S_w and c_w to water phase, S_g and c_g to gas phase; and c_f is the formation compressibility. In Eq. 1.5, k_o is the effective permeability to oil in the presence of the other phases, and μ_o is the oil viscosity; k_g and μ_g refer to the gas phase; and k_w and μ_w refer to the water phase. Because the formation is considered compressible (i.e., pore volume decreases as pressure decreases), porosity is not a constant in Eq. 1.3 as it was assumed to be in Eqs. 1.1 and 1.2.

Solutions to diffusivity equation

This section deals with useful solutions to the diffusivity equation (Section 1.2) describing the flow of a slightly compressible liquid in a porous medium. We also have some comments on solutions to Eqs. 1.2 and 1.3.

There are four solutions to Eq. 1.1 that are particularly useful in well testing: the solution for a bounded cylindrical reservoir; the solution for an infinite reservoir with a well considered to be a line source with zero wellbore radius; the pseudosteady-state solution; and the solution that includes wellbore storage for a well in an infinite reservoir. Before we discuss these solutions, however, we should summarize the assumptions that were necessary to develop Eq. 1.1: homogeneous and isotropic porous medium of uniform thickness; pressure-independent rock and fluid properties; small pressure gradients; radial flow; applicability of Darcy's law (sometimes called laminar flow); and negligible gravity forces. We will introduce further assumptions to obtain solutions to Eq. 1.1.

Bounded Cylindrical Reservoir

Solution of Eq. 1.1 requires that we specify two boundary conditions and an initial condition. A realistic and practical solution is obtained if we assume that (1) a well produces at constant rate, qB,into the wellbore (q refers to flow rate in STB/D at surface conditions, and B is the formation volume factor in RB/STB); (2) the well, with wellbore radius r_w,is centered in a cylindrical reservoir of radius r_e, and that there is no flow across this outer boundary; and (3) before production begins, the reservoir is at uniform pressure, p_i. The most useful form of the desired solution relates flowing pressure, p_wf,at the sandface to time and to reservoir rock and fluid properties. The solution is

.................... (1.6)

where, for efficiency and convenience, we have introduced the dimensionless variables

and

where the α_n are the roots of

and where J₁and Y₁are Bessel functions. (Total compressibility, c_t,is used in all equations in this chapter because even formations that produce a single-phase oil contain an immobile water phase and have formation compressibility.)

The reader unfamiliar with Bessel functions should not be alarmed at this equation. It will not be necessary to use Eq. 1.6 in its complete form to calculate numerical values of p_wf;instead, we will use limiting forms of the solution in most computations. The most important fact about Eq. 1.6 is that, under the assumptions made in its development, it is an exact solution to Eq. 1.1. It sometimes is called the van Everdingen-Hurst constant-terminal-rate solution.² Appendix C discusses this solution more completely. Because it is exact, it serves as a standard with which we may compare more useful (but more approximate) solutions. One such approximate solution follows.

Infinite Cylindrical Reservoir With Line-Source Well

Assume that (1) a well produces at a constant rate, qB;(2) the well has zero radius; (3) the reservoir is at uniform pressure, p_i, before production begins; and (4) the well drains an infinite area (i.e., that p → p_i as r →∞). Under those conditions, the solution to Eq. 1.1 is

.................... (1.7)

where the new symbols are p,the pressure (psi) at distance r (feet) from the well at time t (hours), and

the Ei function or exponential integral.

Before we examine the properties and implications of Eq. 1.7, we must answer a logical question: Since Eq. 1.6 is an exact solution and Since Eq. 1.7 clearly is based on idealized boundary conditions, when (if ever) are pressures calculated at radius r_w from Eq. 1.7 satisfactory approximations to pressures calculated from Eq. 1.6? Analysis of these solutions shows³ that the Ei-function solution is an accurate approximation to the more exact solution for time . For times less than , the assumption of zero well size (i.e., assuming the well to be a line source or sink) limits the accuracy of the equation; at times greater than , the reservoir's boundaries begin to affect the pressure distribution in the reservoir, so that the reservoir is no longer infinite acting.

A further simplification of the solution to the flow equation is possible: for x < 0.02, Ei(– x) can be approximated with an error less than 0.6% by

.................... (1.8)

To evaluate the Ei function, we can use Table 1.1 for 0.02 < x ≤ 10.9. For x ≤ 0.02, we use Eq. 1.8; and for x > 10.9, Ei(–x)can be considered zero for applications in well testing.

In practice, we find that most wells have reduced permeability (damage) near the wellbore resulting from drilling or completion operations. Many other wells are stimulated by acidization or hydraulic fracturing. Eq. 1.7 fails to model such wells properly; its derivation holds the explicit assumption of uniform permeability throughout the drainage area of the well up to the wellbore. Hawkins⁴ pointed out that if the damaged or stimulated zone is considered equivalent to an altered zone of uniform permeability (k_s)and outer radius (r_s), the additional pressure drop across this zone (∆p_s)can be modeled by the steady-state radial flow equation (see Fig. 1.1). Thus,

.................... (1.9)

TABLE 1.1* – VALUES OF THE EXPONENTIAL INTEGRAL, –Ei(–x)

Fig. 1.1 –Schematic of pressure distribution near wellbore.

Eq. 1.9 simply states that the pressure drop in the altered zone is inversely proportional to k_s rather than to k and that a correction to the pressure drop in this region (which assumed the same permeability, k, as in the rest of the reservoir) must be made. Combining Eqs. 1.7 and 1.9, we find that the total pressure drop at the wellbore is

For r = r_w,the argument of the Ei function is sufficiently small after a short time that we can use the logarithmic approximation; thus, the drawdown is

It is convenient to define a skin factor, s,in terms of the properties of the equivalent altered zone:

.................... (1.10)

Thus, the drawdown is

.................... (1.11)

Eq. 1.10 provides some insight into the physical significance of the sign of the skin factor. If a well is damaged (k_s < k),s will be positive, and the greater the contrast between k_s and k and the deeper into the formation the damage extends, the larger the numerical value of s. There is no upper limit for s. Some newly drilled wells will not flow at all before stimulation; for these wells, k_s ≃ 0 and s → ∞. If a well is stimulated (k_s > k),s will be negative, and the deeper the stimulation, the greater the numerical value of s. Rarely does a stimulated well have a skin factor less than –7 or –8, and such skin factors arise only for wells with deeply penetrating, highly conductive hydraulic fractures. We should note finally that, if a well js neither damaged nor stimulated (k = k_s), s = 0. We caution the reader that Eq. 1.10 is best applied qualitatively; actual wells rarely can be characterized exactly by such a simplified model.

Before leaving the discussion of skin factor, we should point out that an altered zone near a particular well affects only the pressure near that well – i.e., the pressure in the unaltered formation away from the well is not affected by the existence of the altered zone. Said another way, we use Eq. 1.11 to calculate pressures at the sandface of a well with an altered zone, but we use Eq. 1.7 to calculate pressures beyond the altered zone in the formation surrounding the well. We have presented no simple equations that can be used to calculate pressures for radius, r, such that r_w < r < r_s, but this will offer no difficulties in well test analysis.

Example 1.1 – Calculation of Pressures Beyond the Wellbore Using the Ei-Function Solution

Problem. A well and reservoir have the following characteristics: The well is producing only oil; it is producing at a constant rate of 20 STB/D. Data describing the well and formation are

μ	=	0.72 cp,
k	=	0.1 md,
ct	=	1.5 × l0–5psi–1
pi	=	3,000 psi,
re	=	3,000 ft,
rw	=	0.5 ft,
Bo	=	1.475 RB/STB,
h	=	150 ft,
ϕ	=	0.23, and
s	=	0.

Calculate the reservoir pressure at a radius of 1 ft after 3 hours of production; then, calculate the pressure at radii of 10 and 100 ft after 3 hours of production.

Solution. The Ei function is not an accurate solution to flow equations until . Here,

Thus, we can use Eq. 1.7 with satisfactory accuracy if the reservoir is still infinite acting at this time. The reservoir will act as an infinite reservoir until .

Here,

Thus, for times less than 211,900 hours, we can use Eq. 1.7. At a radius of 1 ft,

At a radius of 10 ft,

In this calculation, we find the value of the Ei function from Table 1.1. Note, as indicated in the table, that it is a negative quantity.

At a radius of 100 ft,

Here we note that for an argument of 78.49, the Ei function is essentially zero.

Pseudosteady-State Solution. We now discuss the next solution to the radial diffusivity equation that we will use extensively in this introduction to well test analysis. Actually, this solution (the pseudosteady-state solution) is not new. It is simply a limiting form of Eq. 1.6, which describes pressure behavior with time for a well centered in a cylindrical reservoir of radius r_e. The limiting form of interest is that which is valid for large times, so that the summation involving exponentials and Bessel functions is negligible; after this time