You must log in to edit PetroWiki. Help with editing
Content of PetroWiki is intended for personal use only and to supplement, not replace, engineering judgment. SPE disclaims any and all liability for your use of such content. More information
Message: PetroWiki is moving to OnePetro! Please visit PetroWiki's new home here.
Rheometer
A rheometer is a device that measures the way a viscous fluid flows in response to applied forces.
The relation between the strain and stress tensors is an important information when solving the Navier-Stokes flow momentum conservation equation:
where is the velocity vector, t is time, is the mass density, is the pressure, is the stress tensor, is the gravitational field and represents external body force on the fluid. Using the generalized Newtonian fluid convention, the relationship between stress and strain rate tensors is:
where is the strain rate tensor and is the effective viscosity, which is a function of the shear rate () and possible time. The shear rate is the second invariant of the strain rate tensor:
where are the components of the strain rate tensor.
It is the purpose of a rheometer to measure the strain-stress relation of a particular viscous fluid, i.e., .
Rheometer Types
There are essentially four types of shear geometries:
- Couette drag plate flow
- Cylindrical flow
- Poiseuille flow in a tube
- Plate-plate flow
Couette Concentric Cylindrical Rheometer
A typical rheometer geometry used in the pretroleum industry is the Couette concentric cylindrical rheometer. This correspnonds to the rheometer type 1 in the previous list. The rheometer is constituted of a concentric cylindrical bob inside a cylindrical cup. There are two possible arrangements for the rotating element:
- a rotating cylinder, called the rotor, rotates inside a fixed cup around a fixed bob (this is the principle used in the Model 35 rheometer used for the measurment of drilling fluids at the rig site).
- the bob rotates inside a fixed cup (this is a typical configuration for scientific rheometers)
In both cases the rheometer measures the torque on the bob. The rotational speed of the rotating element is varied to obtain different shear conditions.
The possible rotational speeds can either be fixed when using a mechanical system or adjustable when using an electronic speed controller. A Model 35 rheometer has typically 6 or 8 speeds. The speeds used by an Anton Paar MCR301 or MCR302 rheometer are user-controllable.
The relation between the rotation speed and the shear rate is:
where is the angular velocity, is the radial distance, and are respectively the radius of the bob and the radius of cup or rotor. This can be re-written as :
where is the shear stress at the wall of the bob and is the shear stress at the wall of the cup or rotor [1].
For a Newtonian fluid, the conversion from the angular velocity to the shear rate at the wall of the bob is constant : where and is the shear rate at the wall of the bob.
For a Model 35 in the configuration R1B1, mm, mm and when converting angular velocity to RPM. It should be noted that the ISO-3219 convention is to use the average shear rate in the gap. For a Newtonian fluid, where is the average shear rate in the gap. This is the convention used by certain scientific rheometers like those from Anton Paar. For non-Newtonian fluids, the conversion between the angular velocity and the shear rate at the wall depends on the rheological behavior. Skadsem and Saasen [2] provides a method to calculate the shear rate at the wall for a fluid that follows a Herschel-Bulkley rheological behavior, i.e., where is the yield stress, is the consistency index and is the flow behavior index.
The torque on the bob is the integral of the shear stress at the wall: where is the torque on the bob, is the surface of the bob. Considering that the bob is cylindrical, the torque can be be related to the surface of a cylinder where is the height of the bob. However, the shear stress at the wall also applies on the top and bottom of the bob, and to account for these end effects, it is often considered that the height of the bob is slightly longer than its true value:
where is the torque on the bob and is a correction factor for the end effects.
For Newtonian fluids, is constant and is equal to 0.064 for a Model 35 [3] and 0.1 for an Anton Paar MCR301/302. However, an Anton Paar rheometer provides the average shear stress in the gap between the bob and the cup, as according to the ISO-3219 convention. The relationship between the two shear stresses is:
where is the average shear stress in the gap. For non-Newtonian fluids, depends on the rheological behavior. Lac and Parry [4] have made computational fluid dynamics (CFD) simulations for Herschel-Bulkley fluids with different configurations of the Model 35 rheometer (R1B1, R1B2 and R1B5) and provided formulas to estimate the end-effect correction factor for that type of rheometer.
Both the shear rate correction from Skadsem and Saasen and the end-effects corrections from Lac and Parry are implemented in C# and made available as open source by the SPE sub-committee Open Source Drilling Community. The code is available on github here. A simple web application running the open-source code is available here.
Pipe Rheometer
In a pipe rheometer, the fluid flows into a cylindrical pipe and the pressure loss along the pipe is measured. This corresponds to the second type of rheometer in the above classification. The flowrate is varied and/or the fluid passes through multiple pipe sizes to create different shear conditions.
References
- ↑ Krieger, Irvin M. and Elrod, Harold. 1953. Direct Determination of the Flow Curves of Non‐Newtonian Fluids. II. Shearing Rate in the Concentric Cylinder Viscometer. Journal of Applied Physics 24 (2): 134-136. https://aip.scitation.org/doi/abs/10.1063/1.1721226.
- ↑ Skadsem, Hans Joakim and Saasen, Arild. 2019. Concentric cylinder viscometer flows of Herschel-Bulkley fluids. Applied Rheology 29 (1): 173-181. https://doi.org/10.1515/arh-2019-0015.
- ↑ Kelessidis, V. C., Maglione, R., and Bandelis, G. 2010. On the end-effect correction for Couette type oil-field direct-indicating viscometers for Newtonian and non-Newtonian fluids. Journal of Petroleum Science and Engineering 71 (1): 37-46. https://www.sciencedirect.com/science/article/pii/S0920410510000021.
- ↑ Lac, Étienne and Parry, Andrew. 2017. Non-Newtonian end-effects in standard oilfield rheometers. Journal of Rheology 61 (4): 833-843. https://sor.scitation.org/doi/abs/10.1122/1.4986925.
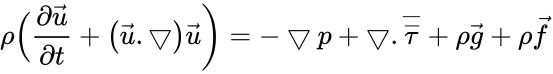
 is the velocity vector, t is time,
is the velocity vector, t is time,  is the mass density,
is the mass density,  is the pressure,
is the pressure, 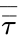 is the stress tensor,
is the stress tensor,  is the gravitational field and
is the gravitational field and 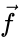 represents external body force on the fluid. Using the generalized Newtonian fluid convention, the relationship between stress and strain rate tensors is:
represents external body force on the fluid. Using the generalized Newtonian fluid convention, the relationship between stress and strain rate tensors is:
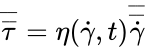
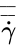 is the strain rate tensor and
is the strain rate tensor and 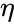 is the effective viscosity, which is a function of the shear rate (
is the effective viscosity, which is a function of the shear rate (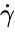 ) and possible time. The shear rate is the second invariant of the strain rate tensor:
) and possible time. The shear rate is the second invariant of the strain rate tensor:
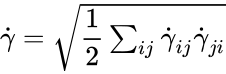
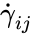 are the components of the strain rate tensor.
are the components of the strain rate tensor.
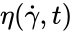 .
.

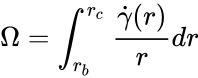
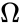 is the angular velocity,
is the angular velocity, 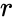 is the radial distance,
is the radial distance, 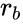 and
and 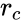 are respectively the radius of the bob and the radius of cup or rotor. This can be re-written as :
are respectively the radius of the bob and the radius of cup or rotor. This can be re-written as :
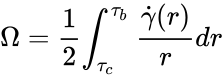
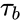 is the shear stress at the wall of the bob and
is the shear stress at the wall of the bob and 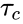 is the shear stress at the wall of the cup or rotor
is the shear stress at the wall of the cup or rotor 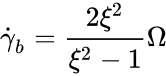 where
where 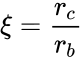 and
and 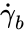 is the shear rate at the wall of the bob.
is the shear rate at the wall of the bob.
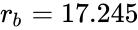 mm,
mm, 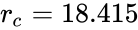 mm and
mm and 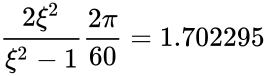 when converting angular velocity to RPM. It should be noted that the ISO-3219 convention is to use the average shear rate in the gap. For a Newtonian fluid,
when converting angular velocity to RPM. It should be noted that the ISO-3219 convention is to use the average shear rate in the gap. For a Newtonian fluid, 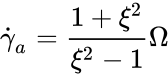 where
where 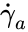 is the average shear rate in the gap. This is the convention used by certain scientific rheometers like those from Anton Paar. For non-Newtonian fluids, the conversion between the angular velocity and the shear rate at the wall depends on the rheological behavior. Skadsem and Saasen
is the average shear rate in the gap. This is the convention used by certain scientific rheometers like those from Anton Paar. For non-Newtonian fluids, the conversion between the angular velocity and the shear rate at the wall depends on the rheological behavior. Skadsem and Saasen 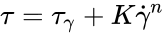 where
where 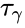 is the yield stress,
is the yield stress,  is the consistency index and
is the consistency index and  is the flow behavior index.
is the flow behavior index.
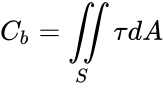 where
where 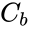 is the torque on the bob,
is the torque on the bob, 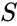 is the surface of the bob. Considering that the bob is cylindrical, the torque can be be related to the surface of a cylinder
is the surface of the bob. Considering that the bob is cylindrical, the torque can be be related to the surface of a cylinder 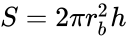 where
where 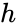 is the height of the bob. However, the shear stress at the wall also applies on the top and bottom of the bob, and to account for these end effects, it is often considered that the height of the bob is slightly longer than its true value:
is the height of the bob. However, the shear stress at the wall also applies on the top and bottom of the bob, and to account for these end effects, it is often considered that the height of the bob is slightly longer than its true value:
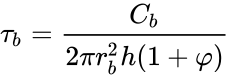
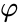 is a correction factor for the end effects.
is a correction factor for the end effects.
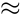 0.064 for a Model 35
0.064 for a Model 35 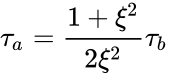
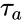 is the average shear stress in the gap. For non-Newtonian fluids,
is the average shear stress in the gap. For non-Newtonian fluids,