Pseudo steady-state

Pseudo-steady state (or pseudo steady-state), is also referred to as "stabilized," or as "steady state in a bounded drainage area." This type of reservoir flow occurs much more frequently than steady-state flow or unsteady-state flow with an expanding drainage radius.

Mechanism

Pseudo-steady state (PSS) flow occurs during the late time region when the outer boundaries of the reservoir are all no flow boundaries. (http://www.fekete.com/SAN/TheoryAndEquations/WellTestTheoryEquations/Pseudo-Steady_State_Flow.htm) This includes not only the case when the reservoir boundaries are sealing faults, but also when nearby producing wells cause no flow boundaries to arise. During the PSS flow regime, the reservoir behaves as a tank. The pressure throughout the reservoir decreases at the same, constant rate. PSS flow does not occur during build-up or falloff tests.

Pseudo-steady state and the approximation technique

The approximation technique addresses the problem of two-dimensional flow of a slightly compressible fluid into a well bisecting a plane vertical fracture. The solution sought is subject to appropriate boundary and initial conditions. Here Ψ is the flow potential, P + ρgH(x̄,ӯ) with H(x̄,ӯ) being vertical height above a hydrostatic datum plane at the point (x̄,ȳ) and we have assumed a homogeneous reservoir of uniform thickness and rock properties which may however be anisotropic. Thus x̄,ȳ are artificial coordinates related to the real rectangular coordinates x,y by

values of the permeability tensor and the coordinate axes are oriented along the principal permeability axes of the formation. This approximation of the flow problem is obtained from Darcy's law, the equation of continuity for fluid of small, constant compressibility and constant viscosity as in Collins. Consistent units are assumed in all equations. Insight into the approximation technique we propose to use for solving the problem of a hydraulically fractured well is provided by examining the well-known "line-sink" solution of this partial differential equation.

where r̄ denotes x̄² + ȳ² and

is defined as the exponential integral function. This describes a well of "zero radius" at the origin in an infinite reservoir of thickness h producing at a constant volumetric rate, q, for t > 0. From this solution, we can show that the flow rate across the "circle" of radius r̄_w is

$q_{w}=q\ e^{-{\phi \mu c{\bar {r}}{_{w}}^{2} \over 4Kt}}$

so for even moderately large values of t, this is an excellent representation for a well of radius r̄_w with a constant rate q. Actually, for the anisotropic case, K_x ~ K_y , the "circle" of fixed radius r̄_w is in fact an ellipse with ratio of axes proportional to ${\sqrt {K_{x}/K_{y}}}$ .

Noteworthy papers in OnePetro

Aminian, K., Ameri, S., Hyman, M.D. 1986. Production Decline Type Curves for Gas Wells Producing Under Pseudo-Steady-State Conditions. Presented at the SPE Eastern Regional Meeting, Columbus. Ohio, 12-14 November. SPE-15933-MS. http://dx.doi.org/10.2118/15933-MS.

Bahadori, A. 2012. Prediction of Skin Factor and Pseudo-steady State Horizontal Wells Productivity for Various Drainage Areas. Presented at the SPETT 2012 Energy Conference and Exhibition, Port-of-Spain, Trinidad, 11-13 June SPE-156278-MS. http://dx.doi.org/10.2118/156278-MS.

German, G.M., Rangel-German, E., Samaniego-Verduzco, F., et al. 2010. Unsteady and Pseudo-steady State Characterization of Matrix and Fracture Systems for Multiple Size Blocks with the Use of Empirical Correlations. Presented at the SPE Latin American and Caribbean Petroleum Engineering Conference, Lima, Peru, 1-3 December.SPE-139204-MS. http://dx.doi.org/10.2118/139204-MS.

Lu, J., Ghedan, S.G. 2010. Pseudo- Steady State Productivity Equation for a Multiple-Wells System in a Sector Fault Reservoir. Presented at the SPE EUROPEC/EAGE Annual Conference and Exhibition, Barcelona, Spain, 14-17 June. SPE-130866-MS. http://dx.doi.org/10.2118/130866-MS.

Onyekonwu, M.O., Ramey, H.J., Brigham, W.E. 1986. Application of Superposition and Pseudo-Steady State Concepts to Thermal Recovery Pressure Tests. Presented at the SPE Annual Technical Conference and Exhibition, New Orleans, 5-8 October.SPE-15536-MS. http://dx.doi.org/10.2118/15536-MS.

Sangsoo, R., Frantz, J.H., Lee, W.J. 1994. New, Simplified Methods for Modeling Multilayer Reservoirs Performing at Pseudo-Steady State. Presented at the SPE Annual Technical Conference and Exhibition, New Orleans, 25-28 September. SPE-28631-MS. http://dx.doi.org/10.2118/28631-MS.

Shahamat, M.S., Mattar, L., Aguilera, R. 2014. A Physics-Based Method for Production Data Analysis of Tight and Shale Petroleum Reservoirs Using Succession of Pseudo-Steady States. Presented at the SPE/EAGE European Unconventional Resources Conference and Exhibition, Vienna, Austria, 25-27 February.SPE-167686-MS. http://dx.doi.org/10.2118/167686-MS.

Slider, H.C. 1966. Application of Pseudo-Steady-State Flow to Pressure-Buildup Analysis. Presented at the SPE Amarillo Regional Meeting, Amarillo, Texas, 27-28 October. SPE-1403-MS. http://dx.doi.org/10.2118/1403-MS.

External links

Lu, J. and Tiab, D. 2011. Pseudo-Steady-State Productivity Formula for a Partially Penetrating Vertical Well in a Box-Shaped Reservoir. Mathematical Problems in Engineering 2 (2) 101-114. http://dx.doi.org/10.1155/2010/907206.

Schlumberger. Pseudosteady state. Oilfield glossary. http://www.glossary.oilfield.slb.com/en/Terms/p/pseudosteady_state.aspx.

See also

Gas lift installation design

PEH:Fluid_Mechanics_for_Drilling

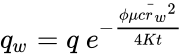
PEH:Gas_Lift