You must log in to edit PetroWiki. Help with editing
Content of PetroWiki is intended for personal use only and to supplement, not replace, engineering judgment. SPE disclaims any and all liability for your use of such content. More information
Strength of casing and tubing
The most important mechanical properties of casing and tubing are burst strength, collapse resistance and tensile strength. These properties are necessary to determine the strength of the pipe and to design a casing string.
Minimum Internal Yield Pressure (MIYP)
If casing is subjected to internal pressure higher than external, it is said that casing is exposed to burst pressure loading. Burst pressure loading conditions occur during well control operations, casing pressure integrity tests, pumping operations, and production operations. The MIYP of the pipe body is determined by the internal yield pressure formula found in API Bull. 5C3, Formulas and Calculations for Casing, Tubing, Drillpipe, and Line Pipe Properties.[1]
....................(1)
where
PB = minimum burst pressure, psi,
Yp = minimum yield strength, psi,
t = nominal wall thickness, in.,
and
D = nominal outside pipe diameter, in.
This equation, commonly known as the Barlow equation, calculates the internal pressure at which the tangential (or hoop) stress at the inner wall of the pipe reaches the yield strength (YS) of the material. The expression can be derived from the Lamé equation for tangential stress by making the thin-wall assumption that D/t >> 1. Most casing used in the oilfield has a D/t ratio between 10 and 35. The factor of 0.875 appearing in the equation represents the allowable manufacturing tolerance of –12.5% on wall thickness specified in API Bull. 5C2, Performance Properties of Casing, Tubing, and Drillpipe.[2] A pressure at MIYP does not mean the pipe will have a burst or rupture failure which only occurs when the tangential stress exceeds the ultimate tensile strength (UTS). So using a yield strength criterion as a measure of pipe internal pressure resistance is inherently conservative. This is particularly true for lower-grade materials such H-40, K-55, and N-80 whose UTS/YS ratio is significantly greater than that of higher-grade materials such as P-110 and Q-125. The effect of axial loading on the internal pressure resistance is discussed later.
Collapse strength
If external pressure exceeds internal pressure, the casing is subjected to collapse. Such conditions may exist during cementing operations, trapped fluid expansion, or well evacuation. Collapse strength is primarily a function of the material's yield strength and its slenderness ratio, D/t. The collapse strength criteria, given in API Bull. 5C3, Formulas and Calculations for Casing, Tubing, Drillpipe, and Line Pipe Properties,[1] consist of four collapse regimes determined by yield strength and D/t . Each criterion is discussed next in order of increasing D/t.
Yield strength collapse
Yield strength collapse is based on yield at the inner wall using the Lamé thick wall elastic solution. This criterion does not represent a "collapse" pressure at all. For thick wall pipes (D/t
<
15±), the tangential stress exceeds the yield strength of the material before a collapse instability failure occurs. ![]() ....................(2) Nominal dimensions are used in the collapse equations. The applicable D/t ratios for yield strength collapse are shown in Table 1.
....................(2) Nominal dimensions are used in the collapse equations. The applicable D/t ratios for yield strength collapse are shown in Table 1.
Plastic collapse
Plastic collapse is based on empirical data from 2,488 tests of K-55, N-80, and P-110 seamless casing. No analytic expression has been derived that accurately models collapse behavior in this regime. Regression analysis results in a 95% confidence level that 99.5% of all pipes manufactured to American Petroleum Institute (API) specifications will fail at a collapse pressure higher than the plastic collapse pressure. The minimum collapse pressure for the plastic range of collapse is calculated by Eq. 3.
The factors A, B, and C and applicable D/t range for the plastic collapse formula are shown in Table 2.
Transition collapse
Transition collapse is obtained by a numerical curve fit between the plastic and elastic regimes. The minimum collapse pressure for the plastic-to-elastic transition zone, PT, is calculated with Eq. 4.
The factors F and G and applicable D/t range for the transition collapse pressure formula, are shown in Table 3.
Elastic collapse
Elastic Collapse is based on theoretical elastic instability failure; this criterion is independent of yield strength and applicable to thin-wall pipe (D/t >
25±). The minimum collapse pressure for the elastic range of collapse is calculated with Eq. 5. ![]() ....................(5) The applicable D/t range for elastic collapse is shown in Table 4.
....................(5) The applicable D/t range for elastic collapse is shown in Table 4.
Most oilfield tubulars experience collapse in the "plastic" and "transition" regimes. Many manufacturers market "high collapse" casing, which they claim has collapse performance properties that exceed the ratings calculated with the formulae in API Bull. 5C3, Formulas and Calculations for Casing, Tubing, Drillpipe, and Line Pipe Properties.[1] This improved performance is achieved principally by using better manufacturing practices and stricter quality assurance programs to reduce ovality, residual stress, and eccentricity. High collapse casing was initially developed for use in the deeper sections of high-pressure wells. The use of high collapse casing has gained wide acceptance in the industry, but its use remains controversial among some operators. Unfortunately, all manufacturers ’ claims have not been substantiated with the appropriate level of qualification testing. If high collapse casing is deemed necessary in a design, appropriate expert advice should be obtained to evaluate the manufacturer’ s qualification test data such as lengths to diameter ratio, testing conditions (end constraints), and the number of tests performed.
Equivalent internal pressure
If the pipe is subjected to both external and internal pressures, the equivalent external pressure is calculated as
where
pe = equivalent external pressure,
po = external pressure,
pi = internal pressure,
and
Δp = po – pi.
To provide a more intuitive understanding of the sense of this relationship, Eq. 6 can be rewritten as
where
D = nominal outside diameter,
and
d = nominal inside diameter.
In Eq. 7, we can see the internal pressure applied to the internal diameter and the external pressure applied to the external diameter. The "equivalent" pressure applied to the external diameter is the difference of these two terms.
Axial strength
The axial strength of the pipe body is determined by the pipe body yield strength formula found in API Bull. 5C3, Formulas and Calculations for Casing, Tubing, Drillpipe, and Line Pipe Properties.[1]
where
Fy = pipe body axial strength (units of force),
Yp = minimum yield strength,
D = nominal outer diameter,
and
d = nominal inner diameter.
Axial strength is the product of the cross-sectional area (based on nominal dimensions) and the yield strength.
Combined stress effects
All the pipe-strength equations previously given are based on a uniaxial stress state (i.e., a state in which only one of the three principal stresses is nonzero). This idealized situation never occurs in oilfield applications because pipe in a wellbore is always subjected to combined loading conditions. The fundamental basis of casing design is that if stresses in the pipe wall exceed the yield strength of the material, a failure condition exists. Hence, the yield strength is a measure of the maximum allowable stress. To evaluate the pipe strength under combined loading conditions, the uniaxial yield strength is compared to the yielding condition. Perhaps the most widely accepted yielding criterion is based on the maximum distortion energy theory, which is known as the Huber-Hencky-Mises yield condition or simply the von Mises stress, triaxal stress, or equivalent stress.[3] Triaxial stress (equivalent stress) is not a true stress. It is a theoretical value that allows a generalized three-dimensional (3D) stress state to be compared with a uniaxial failure criterion (the yield strength). In other words, if the triaxial stress exceeds the yield strength, a yield failure is indicated. The triaxial safety factor is the ratio of the material’s yield strength to the triaxial stress. The yielding criterion is stated as ![]() ....................(9) where
....................(9) where
Yp = minimum yield stress, psi,
σVME = triaxial stress, psi,
σz = axial stress, psi,
σϴ = tangential or hoop stress, psi,
and
σr = radial stress, psi.
The calculated axial stress, σz, at any point along the cross-sectional area should include the effects of:
- Self-weight
- Buoyancy
- Pressure loads
- Bending
- Shock loads
- Frictional drag
- Point loads
- Temperature loads
- Buckling loads
Except for bending/buckling loads, axial loads are normally considered to be constant over the entire cross-sectional area.
The tangential and radial stresses are calculated with the Lamé equations for thick-wall cylinders.
and
where
pi = internal pressure,
po = external pressure,
ri = inner wall radius,
ro = outer wall radius,
and
r = radius at which the stress occurs.
The absolute value of σϴ is always greatest at the inner wall of the pipe and that for burst and collapse loads, where
|
pi – po|
>>
0, then|
σϴ|
>>
|
σr|
. For any pi and po combination, the sum of the tangential and radial stresses is constant at all points in the casing wall. Substituting Eq. 10 and Eq. 11 into Eq. 9, after rearrangements, yields ![]() ....................(12) in which
....................(12) in which  and
and
where
D = outside pipe diameter,
and
t = wall thickness.
Eq. 12 calculates the equivalent stress at any point of the pipe body for any given pipe geometry and loading conditions. To illustrate these concepts, let us consider a few particular cases.
Combined collapse and tension
Assuming that σz
>
0 and σϴ>>
σr and setting the triaxial stress equal to the yield strength results in the next equation of an ellipse. ![]() ....................(13) This is the biaxial criterion used in API Bull. 5C3, Formulas and Calculations for Casing, Tubing, Drillpipe, and Line Pipe Properties,[1] to account for the effect of tension on collapse.
....................(13) This is the biaxial criterion used in API Bull. 5C3, Formulas and Calculations for Casing, Tubing, Drillpipe, and Line Pipe Properties,[1] to account for the effect of tension on collapse. ![]() ....................(14)
where
....................(14)
where
Sa = axial stress based on the buoyant weight of pipe,
and
Yp = yield point.
It is clearly seen that as the axial stress Sa increases, the pipe collapse resistance decreases. Plotting this ellipse, Fig. 1 allows a direct comparison of the triaxial criterion with the API ratings. Loads that fall within the design envelope meet the design criteria. The curved lower right corner is caused by the combined stress effects, as described in Eq. 14.
Combined Burst and Compression Loading
Combined burst and compression loading corresponds to the upper left-hand quadrant of the design envelope. This is the region where triaxial analysis is most critical because reliance on the uniaxial criterion alone would not predict several possible failures. For high burst loads (i.e., high tangential stress and moderate compression), a burst failure can occur at a differential pressure less than the API burst pressure. For high compression and moderate burst loads, the failure mode is permanent corkscrewing (i.e., plastic deformation because of helical buckling). This combined loading typically occurs when a high internal pressure is experienced (because of a tubing leak or a buildup of annular pressure) after the casing temperature has been increased because of production. The temperature increase, in the uncemented portion of the casing, causes thermal growth, which can result in significant increases in compression and buckling. The increase in internal pressure also results in increased buckling.
Combined burst and tension loading
Combined burst and tension loading corresponds to the upper right-hand quadrant of the design envelope. This is the region where reliance on the uniaxial criterion alone can result in a design that is more conservative than necessary. For high burst loads and moderate tension, a burst yield failure will not occur until after the API burst pressure has been exceeded. As the tension approaches the axial limit, a burst failure can occur at a differential pressure less than the API value. For high tension and moderate burst loads, pipe body yield will not occur until a tension greater than the uniaxial rating is reached.
Taking advantage of the increase in burst resistance in the presence of tension represents a good opportunity for the design engineer to save money while maintaining wellbore integrity. Similarly, the designer might wish to allow loads between the uniaxial and triaxial tension ratings. However, great care should be taken in the latter case because of the uncertainty of what burst pressure might be seen in conjunction with a high tensile load (an exception to this is the green cement pressure test load case). Also, connection ratings may limit your ability to design in this region.
Use of triaxal criterion for collapse loading
For many pipes used in the oil field, collapse is an inelastic stability failure or an elastic stability failure independent of yield strength. The triaxial criterion is based on elastic behavior and the yield strength of the material and, hence, should not be used with collapse loads. The one exception is for thick-wall pipes with a low D/t ratio, which have an API rating in the yield strength collapse region. This collapse criterion along with the effects of tension and internal pressure (which are triaxial effects) result in the API criterion being essentially identical to the triaxial method in the lower right-hand quadrant of the triaxial ellipse for thick-wall pipes.
For high compression and moderate collapse loads experienced in the lower left-hand quadrant of the design envelope, the failure mode may be permanent corkscrewing because of helical buckling. It is appropriate to use the triaxial criterion in this case. This load combination typically can occur only in wells that experience a large increase in temperature because of production. The combination of a collapse load that causes reverse ballooning and a temperature increase acts to increase compression in the uncemented portion of the string.
Most design engineers use a minimum wall for burst calculations and nominal dimensions for collapse and axial calculations. Arguments can be made for using either assumption in the case of triaxial design. Most importantly, more so than the choice of dimensional assumptions, is that the results of the triaxial analysis should be consistent with the uniaxial ratings with which they may be compared.
Triaxial analysis is perhaps most valuable when evaluating burst loads. Hence, it makes sense to calibrate the triaxial analysis to be compatible with the uniaxial burst analysis. This can be done by the appropriate selection of a design factor. Because the triaxial result nominally reduces to the uniaxial burst result when no axial load is applied, the results of both of these analyses should be equivalent. Because the burst rating is based on 87.5% of the nominal wall thickness, a triaxial analysis based on nominal dimensions should use a design factor that is equal to the burst design factor multiplied by 8/7. This reflects the philosophy that a less conservative assumption should be used with a higher design factor. Hence, for a burst design factor of 1.1, a triaxial design factor of 1.25 should be used.
Final triaxal stress considerations
Fig. 2 graphically summarizes the triaxial, uniaxial, and biaxial limits that should be used in casing design along with a set of consistent design factors.
Because of the potential benefits (both cost savings and better mechanical integrity) that can be realized, a triaxial analysis is recommended for all well designs. Specific applications include:
- Saving money in burst design by taking advantage of the increased burst resistance in tension
- Accounting for large temperature effects on the axial load profile in high-pressure, high-temperature wells (this is particularly important in combined burst and compression loading)
- Accurately determining stresses when using thick-wall pipe (D/t<12) (conventional uniaxial and biaxial methods have imbedded thin-wall assumptions)
- Evaluating buckling severity (permanent corkscrewing occurs when the triaxial stress exceeds the yield strength of the material)
While it is acknowledged that the von Mises criterion is the most accurate method of representing elastic yield behavior, use of this criterion in tubular design should be accompanied by a few precautions.
First, for most pipe used in oilfield applications, collapse is frequently an instability failure that occurs before the computed maximum triaxial stress reaches the yield strength. Hence, triaxial stress should not be used as a collapse criterion. Only in thick-wall pipe does yielding occur before collapse.
Second, the accuracy of triaxial analysis is dependent upon the accurate representation of the conditions that exist both for the pipe as installed in the well and for the subsequent loads of interest. Often, it is the change in load conditions that is most important in stress analysis. Hence, an accurate knowledge of all temperatures and pressures that occur over the life of the well can be critical to accurate triaxial analysis.
Sample design calculations
In the examples that are discussed next, burst and collapse criteria are examined. Triaxial stresses are calculated for a variety of load situations to demonstrate how the casing strength formulas and the load formulas are actually used.
Sample burst calculation with triaxal comparison
Assume that we have a 13 3/8-in., 72-lbm/ft N-80 intermediate casing set at 9,000 ft and cemented to surface. The burst differential pressure for this casing is given by Eq. 1.
The load case we will test against is the burst displacement-to-gas case, with formation pressure of 6,000 psi, formation depth at 12,000 ft, and gas gradient equal to 0.1 psi/ft.
According to this calculation, the casing is strong enough to resist this burst pressure. As an additional test, let us calculate the von Mises stress associated with this case. Surface axial stress is the casing weight divided by the cross-sectional area (20.77 in.2) less pressure loads when cemented (assume 15 lbm/gal cement).
The radial stresses for the internal and external radii are the internal and external pressures.
The hoop stresses are calculated by the Lamé formula ( Eq. 10 ).
The von Mises equivalent stress or triaxial stress is given as Eq. 9. Evaluating Eq. 9 at the inside radius and at the outside radius, we have
and
The maximum von Mises stress is at the inside of the 13 3/8-in. casing with a value that is 66% of the yield stress. In the burst calculation, the applied pressure was 89% of the calculated burst pressure. Thus, the burst calculation is conservative compared to the von Mises calculation for this case.
Sample collapse calculation
For the sample collapse calculation, we will test the collapse resistance of a 7-in., 23-lbm/ft P-110 liner cemented from 8,000 to 12,000 ft. Comparing the 7-in. liner properties against the various collapse regimes, it was found that transition collapse was predicted for this liner. The collapse pressure for this liner is calculated from Eq. 4 with the following values for F and G, as taken from Table 3.
The collapse pressure is then given by
To evaluate the collapse of this liner, we need internal and external pressures. Internal pressure is determined with the full evacuation above packer.
The external pressure is based on a fully cemented section behind the 7-in. liner. The external pressure profile is given by the mud/cement mix-water external pressure profile where the liner is assumed to be cemented in 10-lbm/gal mud with an internal mix-water pressure gradient of 0.45.
An equivalent pressure is calculated from pi and po for comparison with the collapse pressure, pc , through use of Eq. 6.
Because pe exceeds pc (4,440 psi), the liner is predicted to collapse. It is not appropriate to calculate a von Mises stress for collapse in this case because collapse in the transitional region is not strictly a plastic yield condition.
Nomenclature
| A | = constant in plastic collapse equation, dimensionless |
| B | = constant in plastic collapse equation, dimensionless |
| C | = constant in plastic collapse equation, psi |
| d | = nominal inside diameter of pipe, in. |
| D | = nominal outside pipe diameter, in. |
| D/t | = slenderness ratio, dimensionless |
| f1, f2, f3 | = terms in combined stress effects for collapse, psi |
| F | = constant in transition collapse equation, dimensionless |
| Fy | = pipe-body axial strength, lbf |
| G | = constant in transition collapse equation, dimensionless |
| G | = shear modulus, psi |
| pe | = equivalent external pressure, psi |
| pi | = internal pressure, psi |
| po | = external pressure, psi |
| PB | = minimum burst pressure, psi |
| PE | = elastic collapse pressure, psi |
| PP | = plastic collapse pressure, psi |
| PYp | = yield strength collapse pressure, psi |
| PT | = transition collapse pressure, psi |
| r | = radial annular clearance, in. |
| ri | = inside radius of the pipe, in. |
| ro | = outside radius of the pipe, in. |
| Sa | = axial stress based on the buoyant weight of pipe, psi |
| t | = nominal wall thickness, in. |
| Yp | = minimum yield stress of pipe, psi |
| Δp | = po – pi , psi |
| σr | = radial stress, psi |
| σVME | = triaxial stress, psi |
| σz | = axial stress, psi |
| σϴ | = tangential or hoop stress, psi |
References
- ↑ 1.0 1.1 1.2 1.3 1.4 API Bull. 5C3, Bulletin for Formulas and Calculations for Casing, Tubing, Drillpipe, and Line Pipe Properties, fourth edition. 1985. Dallas: API.
- ↑ API Bull. 5C2, Bulletin for Performance Properties of Casing, Tubing, and Drillpipe, eighteenth edition. 1982. Dallas: API.
- ↑ Crandall, S.H. and Dahl, N.C. 1959. An Introduction to the Mechanics of Solids. New York City: McGraw-Hill Book Company.
See also
Noteworthy papers in OnePetro
External lilnks
General references
Adams, A.J. and Hodgson, T. 1999. Calibration of Casing/Tubing Design Criteria by Use of Structural Reliability Techniques. SPE Drill & Compl 14 (1): 21-27. SPE-55041-PA. http://dx.doi.org/10.2118/55041-PA.
Brand, P.R., Whitney, W.S., and Lewis, D.B. 1995. Load and Resistance Factor Design Case Histories. Presented at the Offshore Technology Conference, Houston, 1-4 May. OTC-7937-MS. http://dx.doi.org/10.4043/7937-MS.
Chen, Y.-C., Lin, Y.-H., and Cheatham, J.B. 1990. Tubing and Casing Buckling in Horizontal Wells (includes associated papers 21257 and 21308 ). SPE J. 42 (2): 140-141, 191. SPE-19176-PA. http://dx.doi.org/10.2118/19176-PA.
Dawson, R. 1984. Drill Pipe Buckling in Inclined Holes. SPE J. 36 (10): 1734-1738. SPE-11167-PA. http://dx.doi.org/10.2118/11167-PA.
Klementich, P.E., Erich F. 1995. A Rational Characterization of Proprietary High Collapse Casing Grades. Presented at the SPE Annual Technical Conference and Exhibition, Dallas, 22-25 October. SPE-30526-MS. http://dx.doi.org/10.2118/30526-MS.
Manual for Steel Construction, Load and Resistance Factor Design. 1986. Chicago: American Institute of Steel Construction.
Miska, S. and Cunha, J.C. 1995. An Analysis of Helical Buckling of Tubulars Subjected to Axial and Torsional Loading in Inclined Wellbores. Presented at the SPE Production Operations Symposium, Oklahoma City, Oklahoma, USA, 2–4 April. SPE-29460-MS. http://dx.doi.org/10.2118/29460-MS.
Mitchell, R.F. 1999. Buckling Analysis in Deviated Wells: A Practical Method. SPE Drill & Compl 14 (1): 11-20. SPE-55039-PA. http://dx.doi.org/10.2118/55039-PA.
Mitchell, R.F. 1988. New Concepts for Helical Buckling. SPE Drill Eng 3 (3): 303–310. SPE-15470-PA. http://dx.doi.org/10.2118/15470-PA.
Mitchell, R.F.: “Casing Design,” in Drilling Engineering, ed. R. F. Mitchell, vol. 2 of Petroleum Engineering Handbook, ed. L. W. Lake. (USA: Society of Petroleum Engineers, 2006). 287-342.
Prentice, C.M. 1970. "Maximum Load" Casing Design. J. Pet Tech 22 (7): 805-811. SPE-2560-PA. http://dx.doi.org/10.2118/2560-PA.
Rackvitz, R. and Fiessler, B. 1978. Structural Reliability Under Combined Random Load Processes. Computers and Structures 9: 489.
Timoshenko, S.P. and Goodier, J.N. 1961. Theory of Elasticity, third edition. New York City: McGraw-Hill Book Co.
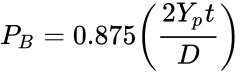 ....................(1)
....................(1)















